日期:2025-07-19 00:14:00
 科创之星
科创之星
早在 1999 年,就跑去俄罗斯设立数学研究所,为啥选这儿?因为俄罗斯数学底蕴深厚,盛产数学大神!华为不惜花重金、下血本,就为招揽这些数学人才,2016 年,华为又在法国设立数学研究所,狂揽菲尔兹奖数学家。
为什么数学好这么招人稀罕,数学好自有黄金屋?
只要掌握了数学思维,就能有逻辑地思考事物。
《原来数学这么有用》的作者鹤崎修功从三岁起就沉浸在“数学沼泽”中的东京大学数学系博士,力图用日常生活中的案例(如A4纸放大、樱花预测、自助餐食物增量等)解读数学原理,让数学不再抽象。
通过这本书邀你领略数学之美、之趣、之用。无论是对数学有恐惧情绪的文科生,还是对数学着迷的理科生,都能在这本书中轻松获得有趣的知识和有效的应试技巧。
来源 | 《原来数学这么有用》
作者 | [日] 鹤崎修功
译者 | 佟凡
01
鹤崎修功:想在数学世界里尽情畅游
我从小就很喜欢数字和算术,上幼儿园的时候尽管自己解不开,但我会沉迷于在格子里抄写数独的答案。抄写数字的感觉就像是画画。
我的父亲是研究生物学的学者,母亲从事声乐工作,不知道为什么这样的两个人会生出我这样一个喜欢数学的孩子,不过我对这种生物学上的问题也基本没有兴趣。
上小学时,我参加了数学奥林匹克竞赛,在那里结识了广中平祐老师和彼得·弗兰克尔先生。
广中老师毕业于京都大学,那里有以他为首的日本最多的菲尔兹奖获奖者。菲尔兹奖被誉为数学领域的诺贝尔奖,所以我曾经有段时间将京都大学作为升学目标。不过,由于高中参加数学奥林匹克竞赛的学生大多进入了东京大学,等我反应过来的时候,我的升学目标已经变成了东京大学。
广中老师的专业领域是格罗滕迪克所创立的代数几何学,当然,东京大学也有很多在这个领域颇负盛名的老师,给我上过课的川又雄二郎老师就是其中一位。除了代数几何学,东京大学还有以研究“算子代数论”著称的河东泰之老师。顺带一提,听说河东泰之老师是俳句作家河东碧梧桐的亲戚。
我原以为东京大学有很多比我更擅长数学的人,担心自己遇到挫折会放弃学习数学科创之星,幸运的是这样的事情并没有发生,直到现在我还在数学领域深耕。
数学可以粗略地分为“代数”“几何”以及“数学分析”, 在这三个分支中我最喜欢代数,所以最终选择了代数的分支“表示论”作为自己的专业,如今我正在研究“李代数表示论”。
另外,我还喜欢研究计算机程序和算法。“李代数表示论”是基础研究,不能直接与现实社会产生联系,但程序可以,比如可以通过程序设计开发出一款对社会有用的软件,这种学习自有其乐趣,不过最吸引我的依然是数学世界的无限奥秘。
我在前文提到了参加数学奥林匹克竞赛的经历,其实我曾挑战过3次,结果次次落败,没能通过地方预选赛,更没能进入世界大赛前的日本预选赛。
如今学完大学博士课程再回顾当初,我觉得只要是自己喜欢的事情,哪怕并非特别擅长,也能坚持下来。当然,有些在数学奥林匹克竞赛中大放异彩的人后来成了数学家,而在数学界,还有更多像我一样几乎没有留下什么成果,但依然选择继续走数学这条道路的人。
所以,我希望大家能做自己真正感兴趣的事情,不要在意别人的目光,尽情沉醉在自己的世界中吧。
02
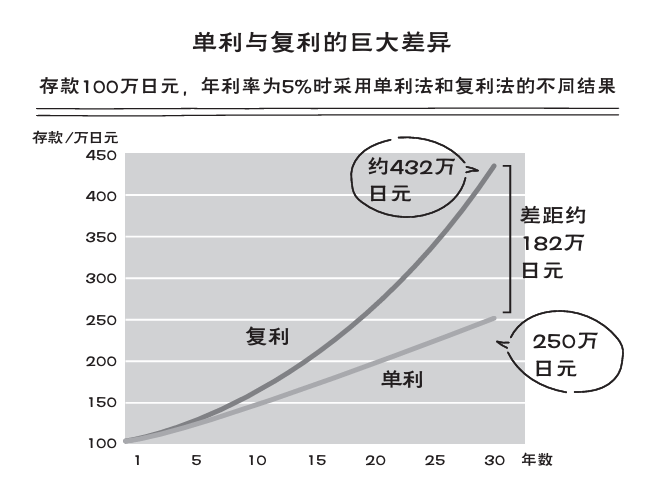
“单利”和“复利”大不相同
银行存款利息有“单利法”和“复利法”两种计算方法。单利法是从存款后的第2年开始,每年只计算最初存入本金的利息;复利法是从存款后第2年开始,每年计算最初存入的本金与之前产生的利息之和的利息。
让我们代入具体数字计算一下吧。假如本金是100万日元,年利率为5%,那么30年后的存款是多少呢?
先用单利法进行计算,100×(1+0.05×30)=250,答案是250万日元。如果用复利法计算,100×1.0530≈432,大约能达到432万日元。也就是说,用复利法计算会比用单利法多出约182万日元的利息。
假设存款金额为y日元,存款时间为x年,年利率为a,未来收入为A日元,单利法的计算公式可以用一次
函数A =y(1+ax) 表示,复利法的计算公式可以用指数函数A =y (1+a)的 x次幂表示。一次函数的图像是一条直线,而指数函数一开始是缓慢上升的曲线,越往右曲线上升的幅度越大。
也就是说,存款时间越长,使用复利法比使用单利法增加的存款金额越多,二者的差距也会越来越大。这正是指数的一大特征,因此用复利法进行计算时应该用指数函数。我们很容易直观理解像一次函数那样的直线变化,而不容易直观理解指数函数的变化。
下面我们来计算一下,每年按照100%的利率收1次复利,以及每年按照10%的利率收10次复利,得到的金额有什么不同。通过计算可知,1年后前者的存款金额增长到原来的2倍,后者的存款金额增长到原来的1.1的10次方倍,即增长到原来的约2.594倍。当每年按照1%的利率收100次复利时,1年后存款金额竟然能够达到原来的约2.705倍,也就是1.01的100次方倍。如果收利息的次数无限细分,就能得到自然常数e。e是无理数,数值为2.71828…。
如果在投资时掌握上述思路,就能实现资产的高效增长。比如在股票投资中投入100万日元,每年有5%的收益,也就是有5万日元的利润。1年后将5万日元立刻取出使用,与留在账户中继续投资,二者后续获得的利润将大为不同。如果取出利息,保持投资金额始终为100万日元,资产在之后每年都只能以单利的方式增长。而如果保留利润继续投资,让投资金额变成105万日元,并且下一年获得的利润同样继续用来投资,资产就能以复利的方式飞速增长。
按照复利规则投资30年,资产会比按照单利规则投资多增加182万日元。
也就是说,在投资时不取出利润而是继续投资的话,就能利用复利效果加快资产增长。
另外,关于复利有一条有趣的法则,叫作“七二法则”。假设年利率为2%,存款金额会在多少年后增长到原来的2倍呢?如果是单利,那就需要50年;如果是复利则需要大约36年,计算方式是用72除以2。实际计算后会发现,36年后的存款金额增长到原来的1.0236≈2.04倍。如果年利率为1%,则用72除以1来计算,大约需要72年;如果年利率为3%,则用72除以3来计算,大约需要24 年;年利率为4%时,可以用72除以4来计算,粗略预测出大约需要18年。
记住七二法则,就能轻松预测自己的存款在未来的增长速度。如果你的目标是晚年存款达到2000万日元,通过计算可知,你需要在距离晚年还有36年时,利用复利规则存入1000万日元,这样当年利率为2%时,你就能在36 年后如愿获得2000万日元。
天才物理学家阿尔伯特·爱因斯坦(1879—1955)也认可复利的作用,据说他曾表示“复利是人类最伟大的发明”。
03
1%的努力和1%的懒惰差距巨大
让我们改变视角,将复利规则代入每天的学习吧。如果你要背诵英语单词,为一年后的高考做准备,假设你每天掌握的英语单词量比前一天增加1%,那么当你最初掌握的英语单词数为1个时,一年后能够达到多少倍呢?
1天后,你掌握的英语单词数为1×1.01个;2天后达到1×1.01×1.01个;3天后为1×1.01×1.01×1.01 个。按照一年有365天计算,一年后你掌握的英语单词数为1乘以1.01 的 365 次方个,即37.7834…个。也就是说,你在一年后掌握的英语单词数量将达到现在的大约38倍。
相反,假设你偷懒,每天忘记1%的英语单词,那么你掌握的英语单词数量在一年后会变成1乘以0.99的365次方个,即0.0255…个,大约变成了现在的0.025倍。
假设你最初掌握的英语单词为100个,如果每天增加1%,那么一年后你掌握的英语单词数量将达到大约3780个;但如果因为偷懒导致每天减少1%,那么一年后你掌握的英语单词数量将会减少到大约2.5个。差距非常大吧,这就是坚持的力量。虽然保持每天努力1%并不简单,但千万不要小看这1%,重要的是要相信每天1%的小小努力不断积累,总有一天能够带来丰厚的成果。

《原来数学这么有用》
作者:[日] 鹤崎修功
译者:佟凡
“数学不是冰冷的公式,而是藏在生活里的魔法!”——从A4纸到樱花预测,从黄金比例到AI算法,带你发现数学的奇妙与实用,轻松掌握数学思维,改变你看世界的方式!
东京大学数学博士教你开启生活中的“数学外挂”!数学是生活的指南,是每天都能用上的超能力!

兴启网配资提示:文章来自网络,不代表本站观点。



